| body | backpack |
|---|---|
| 120 | 26 |
| 187 | 30 |
| 109 | 26 |
| 103 | 24 |
| 131 | 29 |
| 165 | 35 |
| 158 | 31 |
| 116 | 28 |
Scatterplots and correlation
SOC 221 • Lecture 9
Monday, August 4, 2025
Scatterplots and correlation
Overview of Correlation
Looking at the association between variables
- The statistical link between variables
- Tendency for certain types of values of one variable to coincide with certain kinds of values of the other variable
FIRST step in assessing arguments that one variable (independent variable) has a causal impact on another (dependent variable)
We’ve looked for associations between nominal and ordinal variables in bivariate tables
Now we want to measure association for interval variables
STRENGTH
How strong is the tendency for certain values of Y to go with particular values of X?
DIRECTION
Is the association positive or negative?
STATISTICAL SIGNIFICANCE
How certain can we be that the association exists in the population?
Correlation and Scatterplots
Scatterplot: A graph that uses points to simultaneously display the value on two variables for each case in the data
Allows us to picture the association between variables
Example: Association between hiker weight and weight of backpack carried
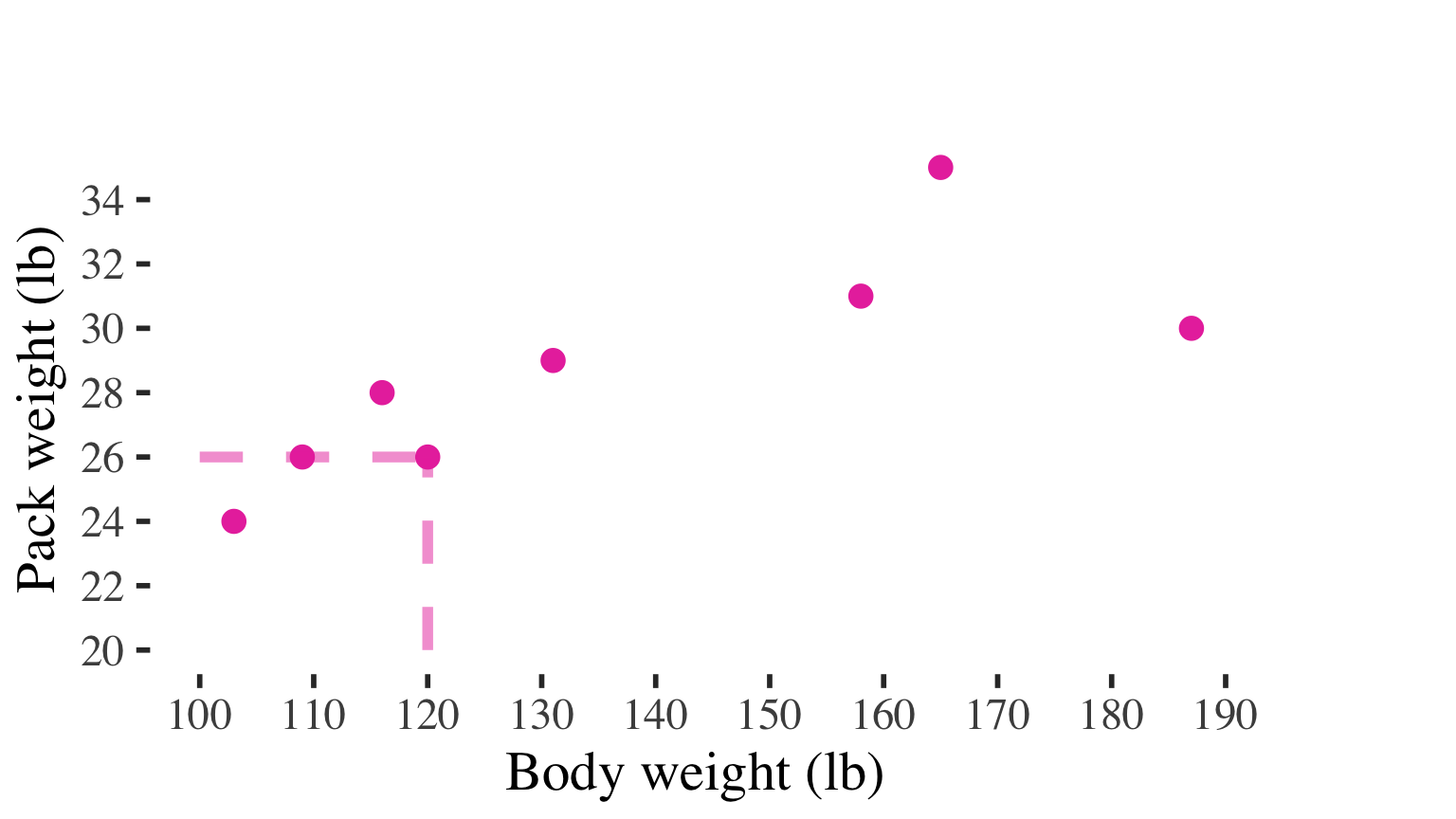
Correlation and Scatterplots
Scatterplot: A graph that uses points to simultaneously display the value on two variables for each case in the data
Allows us to picture the association between variables
Example: Association between hiker weight and weight of backpack carried
| body | backpack |
|---|---|
| 120 | 26 |
| 187 | 30 |
| 109 | 26 |
| 103 | 24 |
| 131 | 29 |
| 165 | 35 |
| 158 | 31 |
| 116 | 28 |
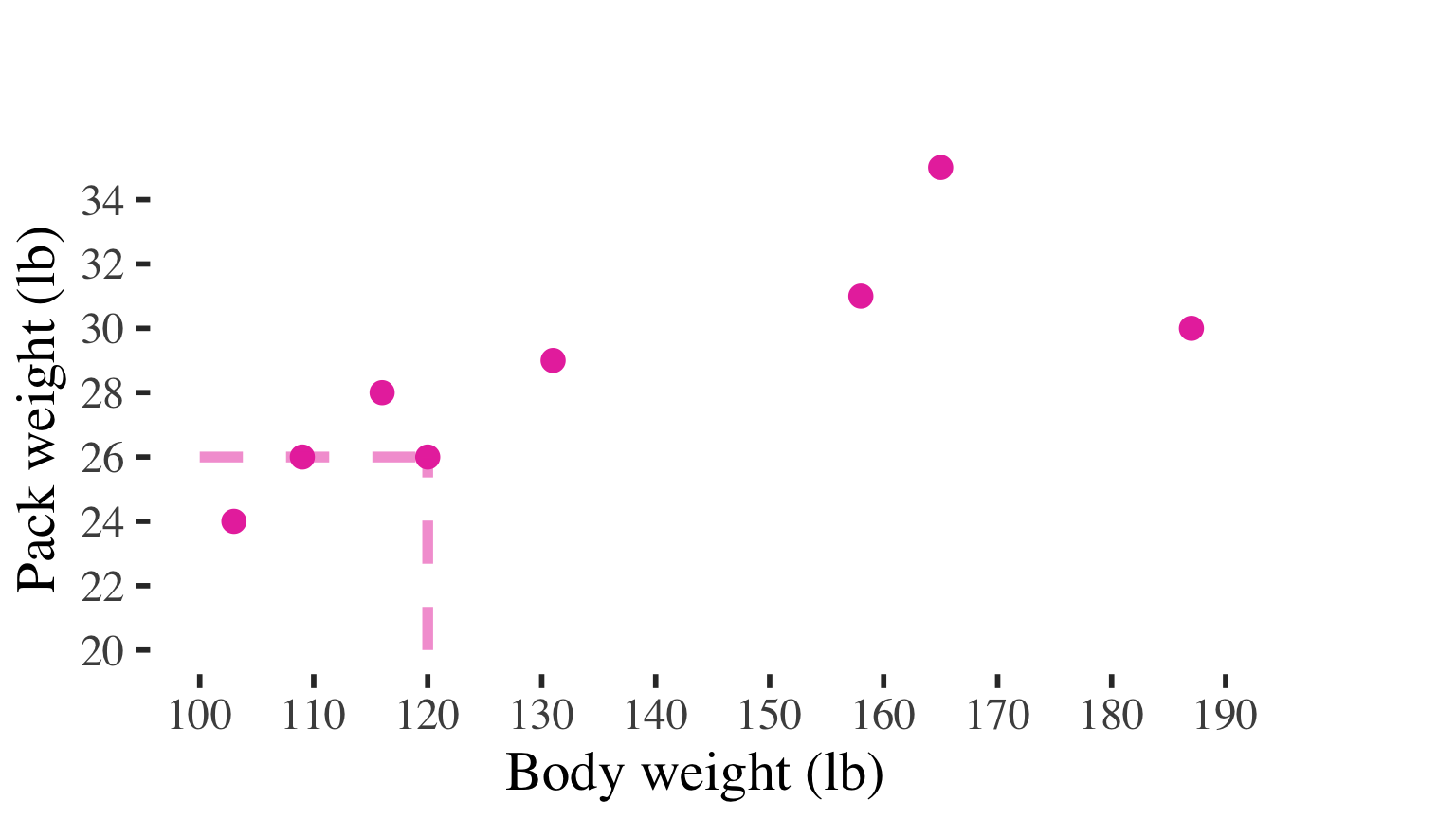
X-axis (horizontal) displays all values in the IV
Y-axis (vertical) displays all values on the DV
Each dot represents a case, positioned along the X and Y axes
Correlation and Scatterplots
Scatterplot: A graph that uses points to simultaneously display the value on two variables for each case in the data
Allows us to picture the association between variables
Example: Association between hiker weight and weight of backpack carried
| body | backpack |
|---|---|
| 120 | 26 |
| 187 | 30 |
| 109 | 26 |
| 103 | 24 |
| 131 | 29 |
| 165 | 35 |
| 158 | 31 |
| 116 | 28 |
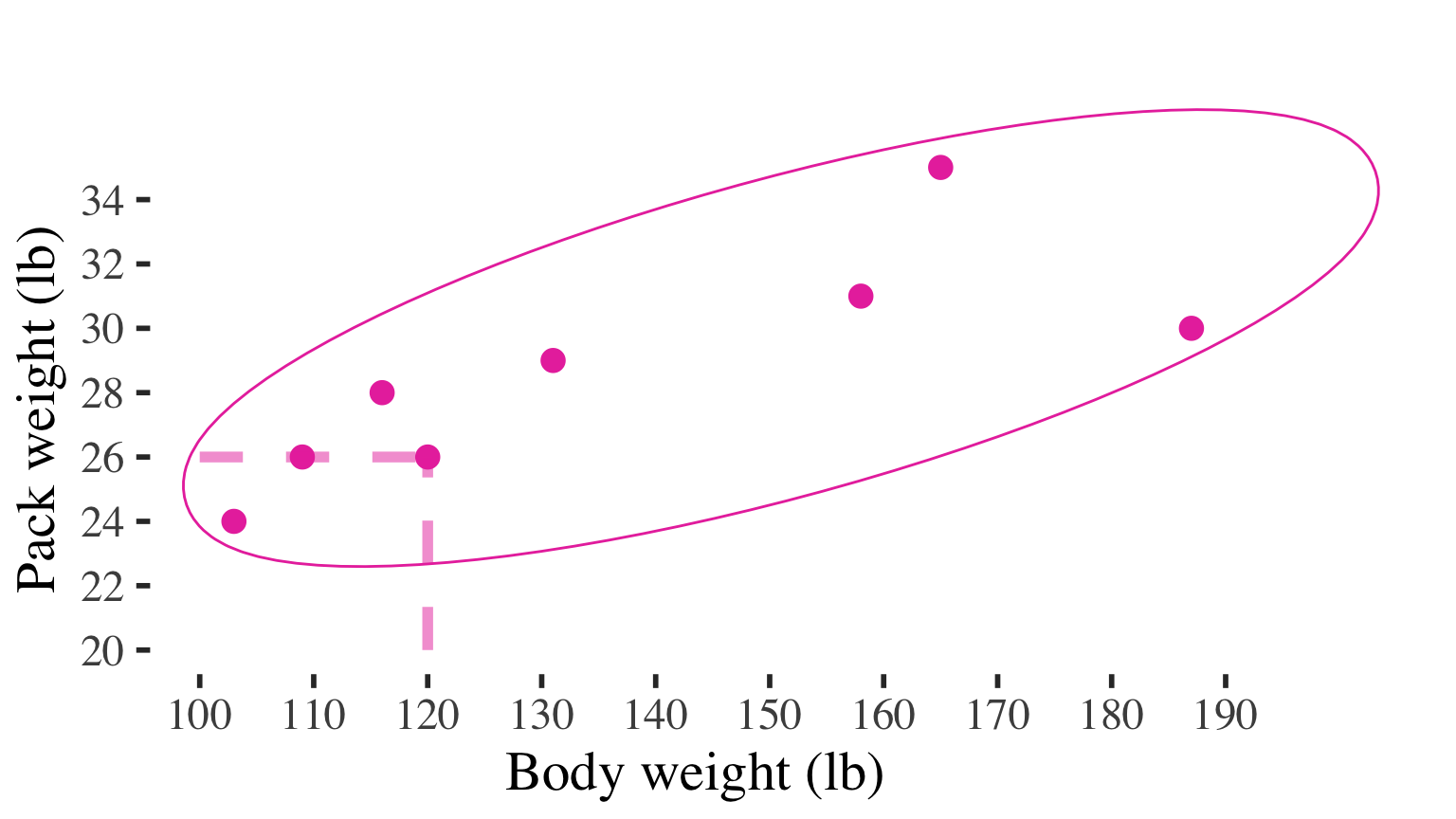
Can see the (positive) association
(high values on one variable tend to go with high values on the other)
Correlation and Regression
The two most common tool for measuring
associations between interval variables
CORRELATION
standardized summary of association between our variables
- does not depend on the units of the variables
- always 0 to |1.0|
- allows for comparison of associations between different pairs of variables
REGRESSION
characterizes the substantive effect of X on Y
- how much Y differs across different values of X
- conveyed in units of our specific independent and dependent variables
Both correlation and regression are based on a description of a line used to characterize data points in a scatterplot
Correlation Coefficient (r)
A measure of association reflecting both the strength and the direction of the association between two interval-level variables
Why it’s helpful
- Simple:
- one number to convey a lot about an association
- Symmetrical:
- correlation of X and Y same as the correlation of Y and X
- Standardized:
- does not depend on the units of the variables
- always ranges from 0 to |1|
- therefore, allows for comparison of bivariate associations between different pairs of variables
Correlation Coefficient (r)
A measure of association reflecting both the strength and the direction of the association between two interval-level variables
Why you need to be careful
- Correlation (and regression) only work well with linear associations
- i.e., scatterplot shows a roughly straight-line pattern
- Correlation ≠ causation
- The observed association might be due to some third “lurking” variable
- i.e., the association might be spurious
- Don’t extrapolate
- Can’t use the observed association to draw conclusions about the association among individuals with values outside of your observed range on the variables
Correlation Coefficient (r)
A measure of association reflecting both the strength and the direction of the association between two interval-level variables
Interpretation
- Sign indicates the direction of the association
- Positive correlation indicates a positive association
- high values on one variable tend to correspond with high values on the other variable
- e.g., education and income have a positive correlation
- Negative correlation indicates a negative association
- high values on one variable tend to correspond with low values on the other variable
- e.g., income and stress have a negative correlation
- Positive correlation indicates a positive association
Correlation Coefficient (r)
A measure of association reflecting both the strength and the direction of the association between two interval-level variables
Interpretation
- Value of the number indicates strength of association
- i.e., how strong is the tendency for certain values on one variable to correspond with certain values on the other?
- Minimum value = 0
- Values close to 0 indicate no association
- Maximum value = 1 or -1
- values close to -1.0 or 1.0 indicate strong relationships
- Rule of thumb (in absolute values):
- 0.00 to 0.30 = weak association
- 0.31 to 0.60 = moderate association
- 0.61 to 1.0 = strong association
Practice
What type of correlations are the following?
- Correlation (r) for education and income = 0.385
moderate and positive - Correlation (r) for education and stress = -0.615
strong and negative - Correlation (r) for hours studied and number of dates = 0.045
weak and positive - Correlation (r) for number of children and number of hours of sleep = -0.421
moderate and negative
Scatterplots allow us to picture the association between variables
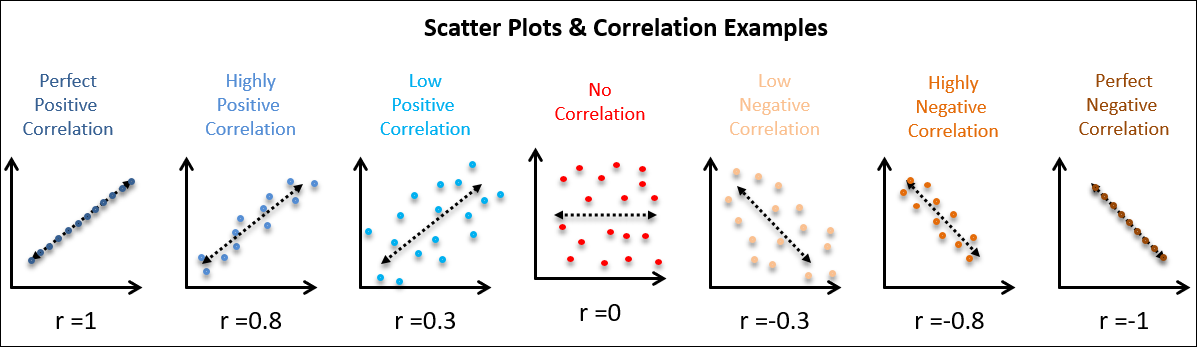
Stronger associations = more tightly clustered points
Weak associations have lots of conditional variation and not much difference in conditional distributions (distribution of the DV across values of the IV)
Strong associations have very little conditional variation and lots of difference in conditional distributions (distribution of the DV across values of the IV)
Making a scatterplot
Example: Do people who study more have more or fewer dates?
| Hours studied | Dates |
|---|---|
| 10 | 1 |
| 15 | 2 |
| 10 | 5 |
| 6 | 1 |
| 2 | 0 |
| 7 | 3 |
| 10 | 4 |
| 12 | 3 |
| 7 | 1 |
| 20 | 3 |

Making a scatterplot
Example: Do people who study more have more or fewer dates?
| Hours studied | Dates |
|---|---|
| 10 | 1 |
| 15 | 2 |
| 10 | 5 |
| 6 | 1 |
| 2 | 0 |
| 7 | 3 |
| 10 | 4 |
| 12 | 3 |
| 7 | 1 |
| 20 | 3 |

Making a scatterplot
Example: Do people who study more have more or fewer dates?
| Hours studied | Dates |
|---|---|
| 10 | 1 |
| 15 | 2 |
| 10 | 5 |
| 6 | 1 |
| 2 | 0 |
| 7 | 3 |
| 10 | 4 |
| 12 | 3 |
| 7 | 1 |
| 20 | 3 |

Making a scatterplot
Example: Do people who study more have more or fewer dates?
| Hours studied | Dates |
|---|---|
| 10 | 1 |
| 15 | 2 |
| 10 | 5 |
| 6 | 1 |
| 2 | 0 |
| 7 | 3 |
| 10 | 4 |
| 12 | 3 |
| 7 | 1 |
| 20 | 3 |
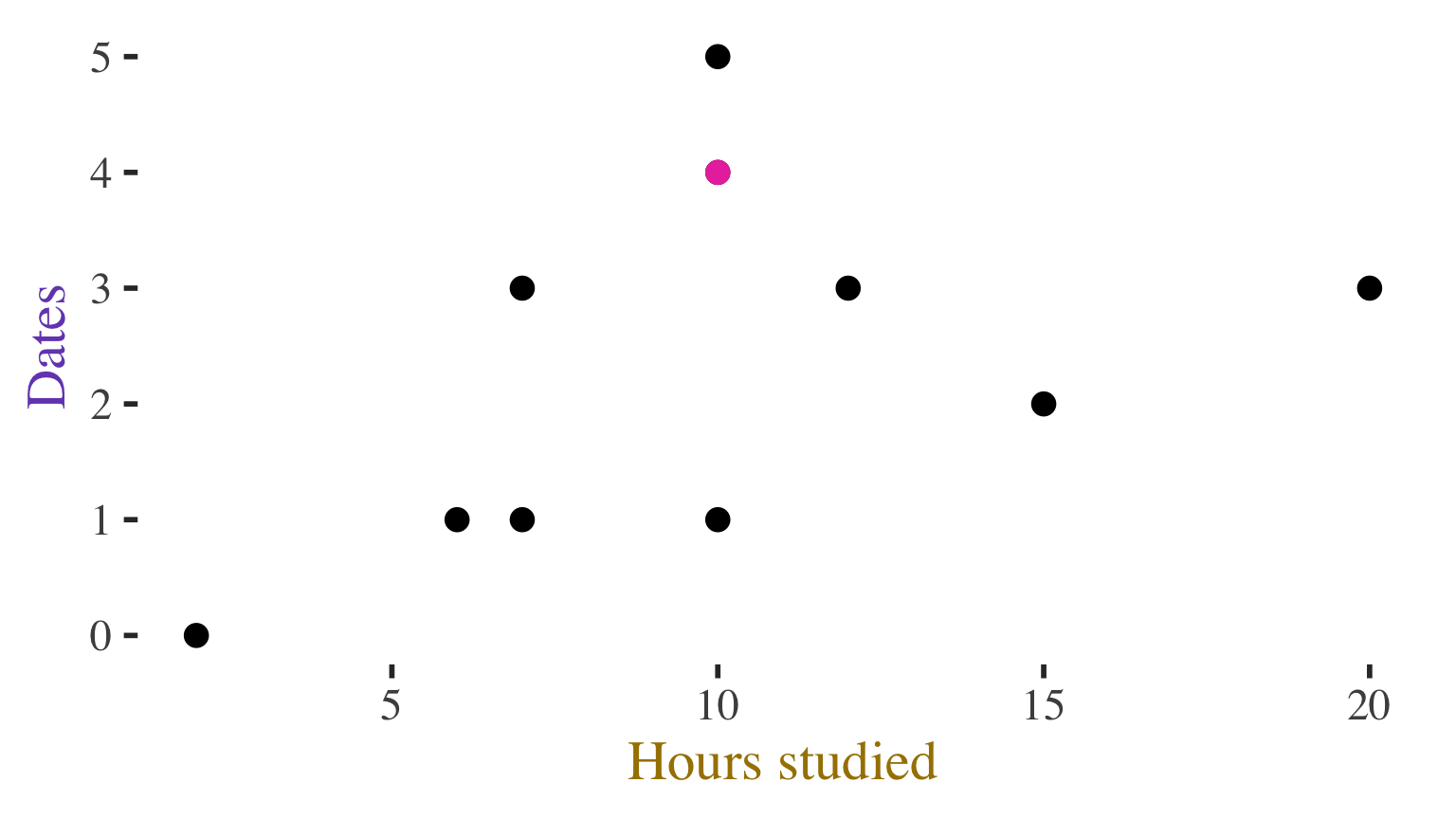
Can see the association
Correlation coefficient allows us to quantify/summarize that association
Calculating correlation coefficient (r)
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
Value of x variable
for an individual
Mean of
x variable
Standard deviation
of x variable
Value of y variable
for an individual
Mean of y variable
Standard deviation
of y variable
Add up for all
individuals
Divide the whole
mess by n-1
Calculating correlation coefficient (r)
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
Just the standardized score on x (i.e. how many standard deviations the individual’s value on x is from the mean of x)
Just the standardized score on y (i.e. how many standard deviations the individual’s value on y is from the mean of y)
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Calculate means and standard
deviations for both variables
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Get the deviation of the x score
from the mean of x
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Get the standardized score of x
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Get the deviation of the y score
from the mean of y
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Get the standardized score of y
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Calculate the product of
standardized scores of x and y
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Do the same thing for every case
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Take the sum of the products of
standardized x and y values
Calculating Correlation Coefficient (r)
Association between hours studied and number of dates
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Hours studied (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 0.10 | 0.02 | -1.30 | -0.83 | -0.02 |
| 2 | 15 | 2 | 5.10 | 1.02 | -0.30 | -0.19 | -0.19 |
| 3 | 10 | 5 | 0.10 | 0.02 | 2.70 | 1.72 | 0.03 |
| 4 | 6 | 1 | -3.90 | -0.78 | -1.30 | -0.83 | 0.64 |
| 5 | 2 | 0 | -7.90 | -1.57 | -2.30 | -1.47 | 2.31 |
| 6 | 7 | 3 | -2.90 | -0.58 | 0.70 | 0.45 | -0.26 |
| 7 | 10 | 4 | 0.10 | 0.02 | 1.70 | 1.08 | 0.02 |
| 8 | 12 | 3 | 2.10 | 0.42 | 0.70 | 0.45 | 0.19 |
| 9 | 7 | 1 | -2.90 | -0.58 | -1.30 | -0.83 | 0.48 |
| 10 | 20 | 3 | 10.10 | 2.01 | 0.70 | 0.45 | 0.90 |
| sum | 99.00 | 23.00 | 4.11 | ||||
| mean | 9.90 | 2.30 | |||||
| st. dev. | 5.02 | 1.57 |
Divide by n-1
\(r = \frac{4.11}{10-1} = 0.456\)
Association between hours studied and number of dates
| Hours studied | Dates |
|---|---|
| 10 | 1 |
| 15 | 2 |
| 10 | 5 |
| 6 | 1 |
| 2 | 0 |
| 7 | 3 |
| 10 | 4 |
| 12 | 3 |
| 7 | 1 |
| 20 | 3 |

Description of the association?
Correlation \(r = 0.456\)
Positive, moderate association
Association between hours studied and number of dates
| Hours studied | Dates |
|---|---|
| 10 | 1 |
| 15 | 2 |
| 10 | 5 |
| 6 | 1 |
| 2 | 0 |
| 7 | 3 |
| 10 | 4 |
| 12 | 3 |
| 7 | 1 |
| 20 | 3 |
Description of the association?
Correlation \(r = 0.456\)
Positive, moderate association
This is the DIRECTION and STRENGTH of
the association in the SAMPLE
Want to know whether there is an association
in the POPULATION (i.e., whether the
observed association is statistically significant)
Need a hypothesis test…
Hypothesis test for correlation
GOAL: We want to know if the association seen in the sample (as revealed by \(r\)) reflects
a real association between the two variables in the population
OR
chance sampling error when in reality the two variables are
not associated in the population
Hypothesis test for correlation
- Check assumptions
- Random sample, variables roughly normally distributed in the population, linear relationship, homoscedasticity
Hypothesis test for correlation
- Check assumptions
- Random sample, variables roughly normally distributed in the population, linear relationship, homoscedasticity
Similar error of prediction (similar spread around the line) at all values of X

Hypothesis test for correlation
- Check assumptions
- Random sample, variables roughly normally distributed in the population, linear relationship, homoscedasticity
- State the hypothesis
- \(H_0: \rho = 0\) (correlation in the population is 0)
- \(H_1: \rho \ne 0\) (correlation in the population is statistically significantly different from 0)
- or \(H_1: \rho \gt 0\) (correlation in the population is statistically significantly greater than 0)
- or \(H_1: \rho \lt 0\) (correlation in the population is statistically significantly less than 0)
- Identify alpha and the critical value of \(r\)
- Use this table to get the ciritical value of \(r\)
- degrees of freedom \((df) = n-2\)
- Calculate the test statistic
- Use \(r\) calculated from the sample
- Make a decision
- Reject or fail to reject null hypothesis
- Make a statement about the implications for the population
Hypothesis test for correlation
- Check assumptions
- Random sample, variables roughly normally distributed in the population, linear relationship, homoscedasticity
- State the hypothesis
- \(H_0: \rho = 0\) (correlation in the population is 0)
- \(H_1: \rho \ne 0\) (correlation in the population is statistically significantly different from 0)
- or \(H_1: \rho \gt 0\) (correlation in the population is statistically significantly greater than 0)
- or \(H_1: \rho \lt 0\) (correlation in the population is statistically significantly less than 0)
- Identify alpha and the critical value of \(r\)
- Use this table to get the ciritical value of \(r\)
- degrees of freedom \((df) = n-2\)
- Calculate the test statistic
- Use \(r\) calculated from the sample
- Make a decision
- Reject or fail to reject null hypothesis
- Make a statement about the implications for the population
Association between hours studied and number of dates
\(r = 0.456\)
Positive, moderate association in the sample
1. Check assumptions
- Random sample?
- Variables roughly normally distributed in the population?
- check sample distributions for a clue
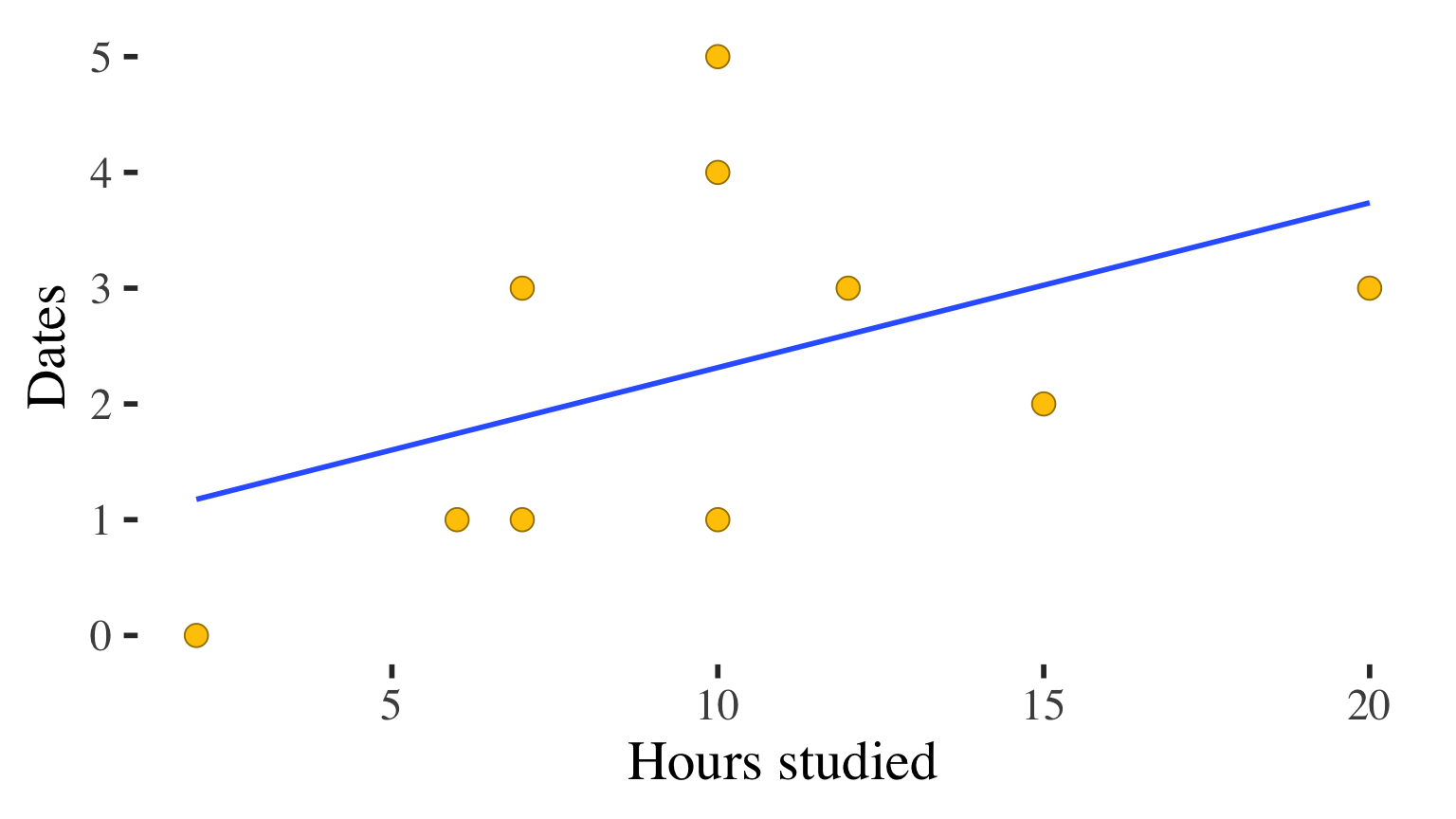
- Linear relationship
- Check scatterplot
- Homoscedasticity
- Similar error of prediction (similar spread around the line) at all values of X
- Check scatterplot
Association between hours studied and number of dates
\(r = 0.456\)
Positive, moderate association in the sample
2. State the hypotheses
3. Decide on alpha and identify
the critical value of \(r\)
4. Calculate the test statistic
5. Make a decision
\(H_0: \rho = 0\)
\(H_1: \rho \ne 0\)
Use alpha = 0.05 by default
Use table for critical values
\(r \text{ observed} = 0.456\)
Since \(r \text{ observed (0.456)}\) < \(r\text{ critical (0.6319)}\),
we FAIL TO REJECT \(H_0\)
2-sided
(direction typically not specified)
We cannot say that there is an association between hours studied and number of dates in the population of students
Practice
- Calculate \(r\)
- Interpret \(r\)
- Test statistical significance of \(r\)
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
Example 1
Association between hours
on TikTok and # of dates?
Example 2
Association between hours playing
video games and # of dates?
| Mean | s | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hours of playing video games |
10 | 5 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 2.00 | 3.50 |
| Hours on TikTok |
0 | 3 | 5 | 15 | 14 | 25 | 1 | 1 | 5 | 22 | 9.10 | 9.21 |
| # of dates |
1 | 2 | 5 | 1 | 0 | 3 | 4 | 3 | 1 | 3 | 2.30 | 1.57 |
Example 1
Association between hours
on TikTok and # of dates?
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Tiktok hours (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | -9.10 | -0.99 | -1.30 | -0.83 | 0.82 |
| 2 | 3 | 2 | -6.10 | -0.66 | -0.30 | -0.19 | 0.13 |
| 3 | 5 | 5 | -4.10 | -0.45 | 2.70 | 1.72 | -0.77 |
| 4 | 15 | 1 | 5.90 | 0.64 | -1.30 | -0.83 | -0.53 |
| 5 | 14 | 0 | 4.90 | 0.53 | -2.30 | -1.47 | -0.78 |
| 6 | 25 | 3 | 15.90 | 1.73 | 0.70 | 0.45 | 0.77 |
| 7 | 1 | 4 | -8.10 | -0.88 | 1.70 | 1.08 | -0.95 |
| 8 | 1 | 3 | -8.10 | -0.88 | 1.70 | 0.45 | -0.39 |
| 9 | 5 | 1 | -4.10 | -0.45 | -1.30 | -0.83 | 0.37 |
| 10 | 22 | 3 | 12.90 | 1.40 | 0.70 | 0.45 | 0.63 |
| sum | 91.00 | 23.00 | -0.71 | ||||
| mean | 9.10 | 2.30 | |||||
| st. dev. | 9.21 | 1.57 |
\(r = \frac{-0.71}{10-1} =\) \(-0.079\)
Interpretation?
Weak negative association between hours on TikTok and number of dates
Statistical significance?
Since absolute value of r-obtained (0.079) is less extreme than the critical value of r (0.6319), we fail to reject \(H_0\) that \(\rho = 0\).
We do not have enough evidence to say that the association observed in the sample exists in the population. It is not statistically significant.
Example 2
Association between hours playing
video games and # of dates?
\[ r = \frac{1}{n-1}\Sigma(\frac{x_i - \bar{x}}{s_x})(\frac{y_i - \bar{y}}{s_y}) \]
| Person | Video game hours (\(x_i\)) | Dates (\(y_i\)) | \(x_i -\bar{x}\) | \(\frac{x_i-\bar{x}}{s_x}\) | \(y_i -\bar{y}\) | \(\frac{y_i-\bar{y}}{s_y}\) | \((\frac{x_i-\bar{x}}{s_x})(\frac{y_i-\bar{y}}{s_y})\) |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 8.00 | 2.29 | -1.30 | -0.83 | 0.82 |
| 2 | 3 | 2 | 3.00 | 0.86 | -0.30 | -0.19 | 0.13 |
| 3 | 5 | 5 | -2.00 | -0.57 | 2.70 | 1.72 | -0.77 |
| 4 | 15 | 1 | -2.00 | -0.57 | -1.30 | -0.83 | -0.53 |
| 5 | 14 | 0 | 3.00 | 0.86 | -2.30 | -1.47 | -0.78 |
| 6 | 25 | 3 | -2.00 | -0.57 | 0.70 | 0.45 | 0.77 |
| 7 | 1 | 4 | -2.00 | -0.57 | 1.70 | 1.08 | -0.95 |
| 8 | 1 | 3 | -2.00 | -0.57 | 1.70 | 0.45 | -0.39 |
| 9 | 5 | 1 | -2.00 | -0.57 | -1.30 | -0.83 | 0.37 |
| 10 | 22 | 3 | -2.00 | -0.57 | 0.70 | 0.45 | 0.63 |
| sum | 91.00 | 23.00 | -4.75 | ||||
| mean | 9.10 | 2.30 | |||||
| st. dev. | 9.21 | 1.57 |
\(r = \frac{-4.75}{10-1} =\) \(-0.528\)
Interpretation?
Moderate negative association between hours of video games played and number of dates.
Statistical significance?
Since absolute value of r-obtained (0.528) is less extreme than the critical value of r (0.6319), we fail to reject \(H_0\) that \(\rho = 0\).
We do not have enough evidence to say that the association observed in the sample exists in the population. It is not statistically significant.
Correlation matrix
Data from a sample of 102 adults results in the correlation matrix to the right
| Age | Hours Worked | Hours on leisure | |
|---|---|---|---|
| Age | 1.00 | 0.28 | -0.40 |
| Hours Worked | 0.28 | 1.00 | -0.61 |
| Hours on leisure | -0.40 | -0.61 | 1.00 |
Interpret the correlation coefficients
Data from a sample of 102 adults results in the correlation matrix to the right
| Age | Hours Worked | Hours on leisure | |
|---|---|---|---|
| Age | 1.00 | 0.28 | -0.40 |
| Hours Worked | 0.28 | 1.00 | -0.61 |
| Hours on leisure | -0.40 | -0.61 | 1.00 |
Interpret the correlation coefficients
Weak positive association between age and hours worked in this sample.
Data from a sample of 102 adults results in the correlation matrix to the right
| Age | Hours Worked | Hours on leisure | |
|---|---|---|---|
| Age | 1.00 | 0.28 | -0.40 |
| Hours Worked | 0.28 | 1.00 | -0.61 |
| Hours on leisure | -0.40 | -0.61 | 1.00 |
Interpret the correlation coefficients
Weak positive association between age and hours worked in this sample.
Moderate negative association between age and leisure hours in this sample.
Data from a sample of 102 adults results in the correlation matrix to the right
| Age | Hours Worked | Hours on leisure | |
|---|---|---|---|
| Age | 1.00 | 0.28 | -0.40 |
| Hours Worked | 0.28 | 1.00 | -0.61 |
| Hours on leisure | -0.40 | -0.61 | 1.00 |
Interpret the correlation coefficients
Weak positive association between age and hours worked in this sample.
Moderate negative association between age and leisure hours in this sample.
Strong negative association between hours worked and leisure hours in this sample.
Data from a sample of 102 adults results in the correlation matrix to the right
| Age | Hours Worked | Hours on leisure | |
|---|---|---|---|
| Age | 1.00 | 0.28 | -0.40 |
| Hours Worked | 0.28 | 1.00 | -0.61 |
| Hours on leisure | -0.40 | -0.61 | 1.00 |
Which of these correlation coefficients is statistically significant at the 0.05 alpha level?
Weak positive association between age and hours worked in this sample.
Moderate negative association between age and leisure hours in this sample.
Strong negative association between hours worked and leisure hours in this sample.
Data from a sample of 102 adults results in the correlation matrix to the right
| Age | Hours Worked | Hours on leisure | |
|---|---|---|---|
| Age | 1.00 | 0.28 | -0.40 |
| Hours Worked | 0.28 | 1.00 | -0.61 |
| Hours on leisure | -0.40 | -0.61 | 1.00 |
Which of these correlation coefficients is statistically significant at the 0.05 alpha level?
\(H_a: \rho \ne 0\)
\(H_0: \rho = 0\)
Compare observed values of \(r\) to the
critical value of \(r\)
critical value of \(r = 0.1946\)
Since all observed values of \(r\) are MORE EXTREME than the critical value of \(r\), we can reject the null hypothesis in each case and conclude that the correlations are likely non-zero IN THE POPULATION (all sample correlations statistically significant)